Line Profile Variations of a Be Star
This Cookbook recipe demonstrates how to simulate the spectral line-profile variations (lpv) of a pulsating Be star, using the MSG Python interface. Synthesizing a spectrum for a pulsating star involves constructing an ensemble of elements representing the stellar surface; subjecting these elements to perturbations from one or more modes; and then integrating the specific intensity over the elements visible to the observer. This process is similar to the disk integration in equation (6) of the MSG Fundamentals chapter, but a further complication is that one must correctly account for Doppler shifts arising from the motion of the elements along the line-of-sight.
The open-source BRUCE and KYLIE codes (Townsend, 1997) perform these tasks. BRUCE constructs and perturbs surface elements, while KYLIE then performs the specific intensity calculations and visible-disk integration. In this recipe the KYLIE functionality is re-implemented in Python.
Preparation
Download be-star-lpv.tar.bz2 and unpack it in your working directory. This archive contains the following items:
elements-*— surface element data produced by BRUCEsg-6678.h5— specgrid file covering the HeI \(\lambda 6678\) line profile [1]input.bdf— BRUCE input file used to createelements-*
Note that input.bdf isn’t needed for the recipe; it’s included for those who wish to recreate elements-*, or are curious about their provenance.
Initialization
To start, import modules and set other parameters:
[1]:
# Import modules
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
import scipy.io as si
import astropy.constants as con
import pymsg
# Set plot parameters
%matplotlib inline
plt.rcParams.update({'font.size': 16})
Create a SpecGrid
Next, create a pymsg.SpecGrid object for interpolating specific intensities:
[2]:
# Create SpecGrid object
specgrid = pymsg.SpecGrid('sg-6678.h5')
Define a Synthesis Function
Now define a function that synthesizes a light curve given the following parameters:
lam — wavelength abscissa array (Angstroms)
d — distance to star (meters)
bruce_file — name of BRUCE output file
specgrid —
pymsg.SpecGridobject
This function is quite simple: it simply adds up the specific intensities from each surface element, appropriately Doppler-shifted and weighted by the elements’s projected area and the observer solid angle.
[3]:
def synthesize_spectrum(lam, d, bruce_file, specgrid):
# Initialize the flux array
n_lam = len(lam)
F = np.zeros(n_lam-1)
# Open the BRUCE output file
with si.FortranFile(bruce_file, 'r') as f:
# Read header
record = f.read_record('<i4', '<f4')
n_vis = record[0][0]
time = record[1][0]
# Read elements and accumulate flux
for i in range(n_vis):
Teff, V_proj, A_proj, g, mu = f.read_reals('<f4')
# Evaluate specific intenensity
x = {'Teff': Teff, 'log(g)': np.log10(g)+2.}
dI = specgrid.intensity(x, mu, lam*(1+V_proj/con.c.value))
# Accumulate flux
F += A_proj * dI * (1./d)**2
# Return the time and flux
return time, F
Evaluate the Spectra
Using this function, evaluate a time-series of spectra:
[4]:
# Set up parameters
d = 10*con.pc.value
lam = np.linspace(6673, 6682, 101)
lam_mid = 0.5*(lam[:-1] + lam[1:])
n_time = 20
# Evaluate spectra
time = []
F = []
for i in range(n_time):
bruce_file = f'elements-{i+1:03d}'
result = synthesize_spectrum(lam, 10*con.pc.value, bruce_file, specgrid)
time += [result[0]]
F += [result[1]]
Plot the Spectra
As a final step, plot the spectra (with a vertical offset between times, to allow comparison):
[5]:
# Plot spectra
plt.figure()
cmap = mpl.colormaps['cool']
fig = plt.figure()
offset=0.2*(np.max(F[0]) - np.min(F[0]))
for i in range(n_time):
plt.plot(lam_mid, 1E8*(F[i]+i*offset), color=cmap(i/(n_time-1)))
plt.xlabel('Wavelength (Angstrom)')
plt.ylabel('Flux (erg/cm^2/s/Angstrom)')
[5]:
Text(0, 0.5, 'Flux (erg/cm^2/s/Angstrom)')
<Figure size 640x480 with 0 Axes>
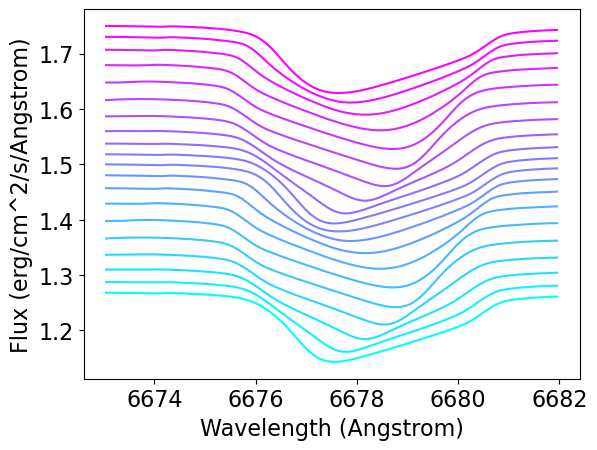
The lpv in the figure take the form of dips of enhanced absorption that travel across the line profile from blue to red. This is similar to the variations observed in pulsating Be stars (see, e.g., Štefl et al. 2003).
Footnotes