Isochrone Color-Magnitude Diagram
This Cookbook recipe demonstrates how to create a color-magnitude diagram (CMD) for an isochrone, using the MSG Python interface.
Preparation
Download isochrone-cmd.tar.bz2 and unpack it in your working directory. This archive contains the following items:
Initialization
To start, import modules and set other parameters:
[1]:
# Import modules
import numpy as np
import matplotlib.pyplot as plt
import astropy.constants as con
import pymsg
import read_mist_models
# Set plot parameters
%matplotlib inline
plt.rcParams.update({'font.size': 16})
Create PhotGrids
Next, create a pair of pymsg.PhotGrid objects for interpolating fluxes in the Johnson B and V bands:
[2]:
# Create PhotGrid objects
photgrid_B = pymsg.PhotGrid('pg-Johnson-B.h5')
photgrid_V = pymsg.PhotGrid('pg-Johnson-V.h5')
Read Isochrone Data
Now read in the isochrone data file and extract the stellar parameters:
[3]:
# Read isochrone data file
iso = read_mist_models.ISO('MIST.iso')
# Extract stellar parameters
Teff = 10**iso.isos[0]['log_Teff']
logg = iso.isos[0]['log_g']
R = 10**iso.isos[0]['log_R']*con.R_sun.value
Reading in: MIST.iso
Evaluate Fluxes
Using these parameters, evaluate the observed flux at 10 parsecs in each band:
[4]:
# Evaluate fluxes
n = len(Teff)
F_B = np.empty(n)
F_V = np.empty(n)
for i in range(n):
# Set up photospheric parameters dict
x = {'Teff': Teff[i],
'log(g)': logg[i]}
# Evaluate fluxes. Use try/execpt clause to deal with
# points that fall outside the grid
try:
F_B[i] = (R[i]/(10*con.pc.value))**2 * photgrid_B.flux(x)
F_V[i] = (R[i]/(10*con.pc.value))**2 * photgrid_V.flux(x)
except (ValueError, LookupError):
F_B[i] = np.NAN
F_V[i] = np.NAN
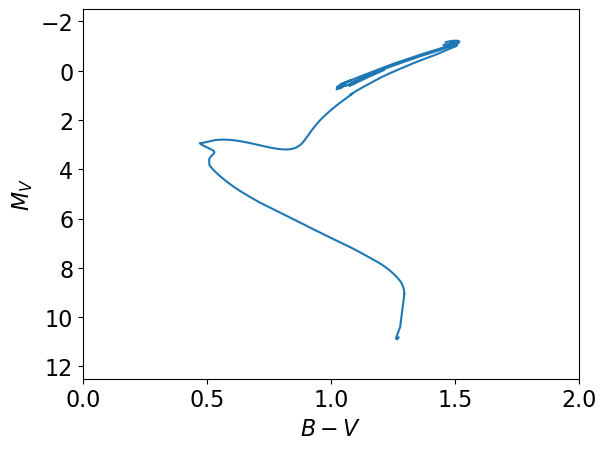
Plot the CMD
As a final step, convert fluxes to (absolute) magnitudes and plot the CMD:
[5]:
plt.figure()
M_B = -2.5*np.log10(F_B)
M_V = -2.5*np.log10(F_V)
plt.plot(M_B-M_V, M_V)
plt.xlim(0, 2)
plt.ylim(12.5,-2.5)
plt.xlabel('$B-V$')
plt.ylabel('$M_V$')
[5]:
Text(0, 0.5, '$M_V$')
Footnotes